In Spring of 2018 I took an abstract algebra course taught by David Hill and Washington State University. It was, to put it bluntly, the single most difficult class I have ever taken. It was also one of the most rewarding courses as it made me feel like an actual mathematician by the time I was done. We broke down our understanding of algebra as a concept and redefined it from scratch using Group Theory. Most of us broke down personally, some of us cried, I personaly wrote a seven page paper in which I worked through on the Ehrenfest Urn problem using a book by Persi Diaconis called Group representations in probability and statistics. I also cried.
The Ehrenfest Urn problem is deceptively simple. Picture two urns (or buckets, or jugs, any container will work) each filled with marbles (or balls, or poker chips, etc.). In the first Urn (Just picture an Urn, it will make this easier), all of the marbles are white. In the second Urn (it doesn’t have to be a funeral Urn filled with ashes, I picture the kind you store coffee in) all the marbles are black. The question is, if we define some type of mixing action, how many times do we need to perform that action before we can expect the Urns to be sufficiently mixed? In order to get a closed form solution, something like “If there are 4 marbles in each Urn we could expect mixture after ‘x’ mixes.” I attempted to employ Group Theory.
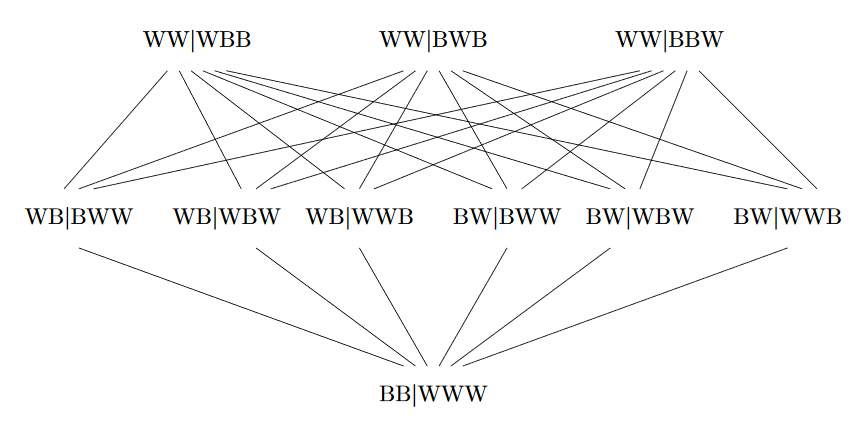
It was a train wreck, but in a very fun and useful way. I started by trying to understand Diaconis’s writing on the subject, realized it was way out of my reach, and instead went about trying to solve the problem from scratch using what I knew about group theory, which wasn’t much. I attempted a few different methods, realized the shortcomings as they failed to help me solve the problem, and eventually settled on the concept of a ‘random walk along the group lattice’. In essence I figured out what all the possible outcomes of a mixing action were for every given Urn starting point and created a map to show how I could move around. Here is a relatively small map for two Urns with only two and three marbles respectively.
Fig 1. A Needlessly complex web of marbles
This solution was not elegant, but it taught me a lot about the importance and power of group theory. It also gave me a huge amount of respect for anyone who understands the subject. My paper on the subject was not great, and it does not read well in the section “Acting on U” but I am immensely proud of it nonetheless. It is a candidate for revision in the future as my own understanding of the subject advances. You can download the full PDF here.